Lab 4: Recursion, Tree Recursion, Python Lists lab04.zip

Due by 11:59pm on Wednesday, September 21.

Recursion/Tree Recursion

Q1: WWPD: Squared Virahanka Fibonacci

Use Ok to test your knowledge with the following “What Would Python Display?” questions:
1
python3 ok -q squared-virfib-wwpd -u✂️

Hint: If you are stuck, make sure to try drawing out the recursive call tree! This is a challenging problem – doing so will really help with understanding how tree recursion works. We strongly encourage trying to draw things out before asking for help from your TA/AIs.

Background: In the Squared Virahanka Fibonacci sequence, each number in the sequence is the square of the sum of the previous two numbers in the sequence. The first 0th and 1st number in the sequence are 0 and 1, respectively. The recursive virfib_sq function takes in an argument n and returns the nth number in the Square Virahanka Fibonacci sequence.

>>> def virfib_sq(n):
>>>     print(n)
>>>     if n <= 1:
>>>         return n
>>>     return (virfib_sq(n - 1) + virfib_sq(n - 2)) ** 2
>>> r0 = virfib_sq(0)
______
>>> r1 = virfib_sq(1)
______
>>> r2 = virfib_sq(2)
______
>>> r3 = virfib_sq(3)
______
>>> r3
______
>>> (r1 + r2) ** 2
______
>>> r4 = virfib_sq(4)
______
>>> r4
______

Q2: Summation

Write a recursive implementation of summation, which takes a positive integer n and a function term. It applies term to every number from 1 to n including n and returns the sum.

Important: Use recursion; the tests will fail if you use any loops (for, while).

def summation(n, term):
    """Return the sum of numbers 1 through n (including n) wíth term applied to each number.
    Implement using recursion!

    >>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
    225
    >>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
    54
    >>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
    62
    >>> # Do not use while/for loops!
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'summation',
    ...       ['While', 'For'])
    True
    """
    assert n >= 1
    "*** YOUR CODE HERE ***"、
    if n==1:
        return term(1)
    return term(n)+summation(n-1,term)

Q3: Pascal’s Triangle

Pascal’s triangle gives the coefficients of a binomial expansion; if you expand the expression (a + b) ** n, all coefficients will be found on the nth row of the triangle, and the coefficient of the ith term will be at the ith column.

Here’s a part of the Pascal’s trangle:

Every number in Pascal’s triangle is defined as the sum of the item above it and the item above and to the left of it. Rows and columns are zero-indexed; that is, the first row is row 0 instead of 1 and the first column is column 0 instead of column 1. For example, the item at row 2, column 1 in Pascal’s triangle is 2.

Now, define the procedure pascal(row, column) which takes a row and a column, and finds the value of the item at that position in Pascal’s triangle. Note that Pascal’s triangle is only defined at certain areas; use 0 if the item does not exist. For the purposes of this question, you may also assume that row >= 0 and column >= 0.

def pascal(row, column):
    """Returns the value of the item in Pascal's Triangle
    whose position is specified by row and column.
    >>> pascal(0, 0)    # The top left (the point of the triangle)
    1
    >>> pascal(0, 5)	# Empty entry; outside of Pascal's Triangle
    0
    >>> pascal(3, 2)	# Row 3 (1 3 3 1), Column 2
    3
    >>> pascal(4, 2)     # Row 4 (1 4 6 4 1), Column 2
    6
    """
    "*** YOUR CODE HERE ***"
    if row<column:
        return 0
    elif column==0 or row==column:
        return 1
    return pascal(row-1, column)+pascal(row-1, column-1)

Q4: Insect Combinatorics

Consider an insect in an M by N grid. The insect starts at the bottom left corner, (1, 1), and wants to end up at the top right corner, (M, N). The insect is only capable of moving right or up. Write a function paths that takes a grid length and width and returns the number of different paths the insect can take from the start to the goal. (There is a closed-form solution to this problem, but try to answer it procedurally using recursion.)

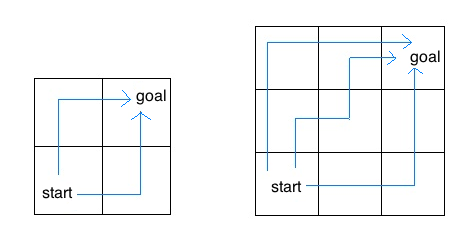
For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).

Hint: What happens if we hit the top or rightmost edge?

def paths(m, n):
    """Return the number of paths from one corner of an
    M by N grid to the opposite corner.

    >>> paths(2, 2)
    2
    >>> paths(5, 7)
    210
    >>> paths(117, 1)
    1
    >>> paths(1, 157)
    1
    """
    "*** YOUR CODE HERE ***"
    if n==1 or m==1:
        return 1
    return paths(m-1,n)+paths(m,n-1)

List Comprehensions

Q5: Couple

Implement the function couple, which takes in two lists and returns a list that contains lists with i-th elements of two sequences coupled together. You can assume the lengths of two sequences are the same. Try using a list comprehension.

Hint: You may find the built in range function helpful.

def couple(s, t):
    """Return a list of two-element lists in which the i-th element is [s[i], t[i]].

    >>> a = [1, 2, 3]
    >>> b = [4, 5, 6]
    >>> couple(a, b)
    [[1, 4], [2, 5], [3, 6]]
    >>> c = ['c', 6]
    >>> d = ['s', '1']
    >>> couple(c, d)
    [['c', 's'], [6, '1']]
    """
    assert len(s) == len(t)
    "*** YOUR CODE HERE ***"
    return [[s[i],t[i]] for i in range(len(s))]

Optional Questions

Recursion

Q6: Double Eights

Write a recursive function that takes in a number n and determines if the digits contain two adjacent 8s. You can assume that n is at least a two-digit number. You may have already done this problem iteratively as an Extra Practice problem in Lab 1.

Hint: Remember what tools you can use in order to isolate digits of a number. If you have trouble figuring out how to implement the recursion, try first finding an iterative solution, and think about how you might be able to turn any loops in recursion.

def double_eights(n):
    """ Returns whether or not n has two digits in row that
    are the number 8. Assume n has at least two digits in it.

    >>> double_eights(1288)
    True
    >>> double_eights(880)
    True
    >>> double_eights(538835)
    True
    >>> double_eights(284682)
    False
    >>> double_eights(588138)
    True
    >>> double_eights(78)
    False
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'double_eights', ['While', 'For'])
    True
    """
    "*** YOUR CODE HERE ***"
    if n<10:
        return False
    if n%10==8 and n//10%10==8:
        return True
    else :
        n=n//10
        return double_eights(n)

List Comprehensions

Q7: Coordinates

Implement a function coords that takes a function fn, a sequence seq, and a lower and upper bound on the output of the function. coords then returns a list of coordinate pairs (lists) such that:

Each (x, y) pair is represented as [x, fn(x)]
The x-coordinates are elements in the sequence
The result contains only pairs whose y-coordinate is within the upper and lower bounds (inclusive)

See the doctest for examples.

Note: your answer can only be one line long. You should make use of list comprehensions!

def coords(fn, seq, lower, upper):
    """
    >>> seq = [-4, -2, 0, 1, 3]
    >>> fn = lambda x: x**2
    >>> coords(fn, seq, 1, 9)
    [[-2, 4], [1, 1], [3, 9]]
    """
    "*** YOUR CODE HERE ***"
    return [[seq[i],fn(seq[i])] for i in range(len(seq)) if fn(seq[i])>=lower and fn(seq[i])<=upper]

Q8: Riffle Shuffle

A common way of shuffling cards is known as the riffle shuffle. The shuffle produces a new configuration of cards in which the top card is followed by the middle card, then by the second card, then the card after the middle, and so forth.

Write a list comprehension that riffle shuffles a sequence of items. You can assume the sequence contains an even number of items.

Hint: There are two ways you can write this as a single list comprension: 1) You may find the expression k%2, which evaluates to 0 on even numbers and 1 on odd numbers, to be alternatively access the beginning and middle of the deck. 2) You can utilize an if expression in your comprehension for the odd and even numbers respectively.

def riffle(deck):
    """Produces a single, perfect riffle shuffle of DECK, consisting of
    DECK[0], DECK[M], DECK[1], DECK[M+1], ... where M is position of the
    second half of the deck.  Assume that len(DECK) is even.
    >>> riffle([3, 4, 5, 6])
    [3, 5, 4, 6]
    >>> riffle(range(20))
    [0, 10, 1, 11, 2, 12, 3, 13, 4, 14, 5, 15, 6, 16, 7, 17, 8, 18, 9, 19]
    """
    "*** YOUR CODE HERE ***"
    return [deck[int(i//2+(len(deck)/2)*(i%2))] for i in range(0,len(deck))]