CS61A Homework 4
easterling
  2023-09-05 21:55:14 2023-09-05 21:55   2024-03-04 21:08:58  

Homework 4: Sequences, Trees hw04.zip

Required questions

Arms-length recursion

Before we get started, a quick comment on recursion with tree data structures. Consider the following function.

1
2
3
4
5
6
7
8
9
def min_depth(t):
    """A simple function to return the distance between t's root and its closest leaf"""
    if is_leaf(t):
        return 0 # Base case---the distance between a node and itself is zero
    h = float('inf') # Python's version of infinity
    for b in branches(t):
        if is_leaf(b): return 1 # !!!
        h = min(h, 1 + min_depth(b))
    return h

The line flagged with !!! is an “arms-length” recursion violation. Although our code works correctly when it is present, by performing this check we are doing work that should be done by the next level of recursion—we already have an if-statement that handles any inputs to min_depth that are leaves, so we should not include this line to eliminate redundancy in our code.

1
2
3
4
5
6
7
8
9
def min_depth(t):
    """A simple function to return the distance between t's root and its closest leaf"""
    if is_leaf(t):
        return 0
    h = float('inf')
    for b in branches(t):
        # Still works fine!
        h = min(h, 1 + min_depth(b))
    return h

Arms-length recursion is not only redundant but often complicates our code and obscures the functionality of recursive functions, making writing recursive functions much more difficult. We always want our recursive case to be handling one and only one recursive level. We may or may not be checking your code periodically for things like this.

Mobiles

Acknowledgements This mobile example is based on a classic problem from MIT Structure and Interpretation of Computer Programs, Section 2.2.2.

image

We are making a planetarium mobile. A mobile is a type of hanging sculpture. A binary mobile consists of two arms. Each arm is a rod of a certain length, from which hangs either a planet or another mobile. For example, the below diagram shows the left and right arms of Mobile A, and what hangs at the ends of each of those arms.

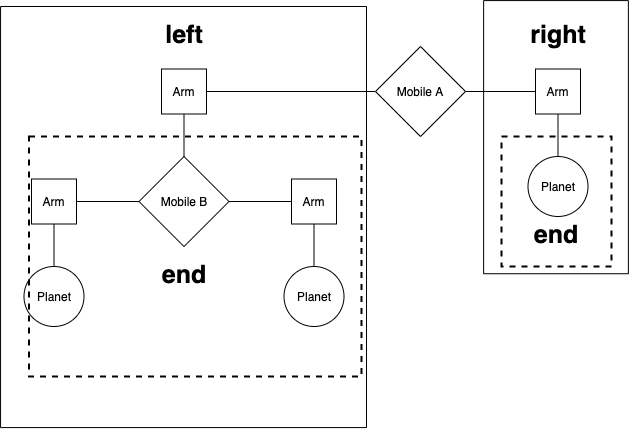
image

We will represent a binary mobile using the data abstractions below.

  • A mobile must have both a left arm and a right arm.
  • An arm has a positive length and must have something hanging at the end, either a mobile or planet.
  • A planet has a positive mass, and nothing hanging from it.

Q2: Weights

Below are the implementations of the various data abstractions used in mobiles. The mobile and arm data abstractions have been completed for you.

Your job is to implement the planet data abstraction by completing the planet constructor and the mass selector so that a planet is represented using a two-element list where the first element is the string 'planet' and the second element is its mass.

Implementation of the Mobile Data Abstraction (for your reference, no need to do anything here):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def mobile(left, right):
    """Construct a mobile from a left arm and a right arm."""
    assert is_arm(left), "left must be a arm"
    assert is_arm(right), "right must be a arm"
    return ['mobile', left, right]

def is_mobile(m):
    """Return whether m is a mobile."""
    return type(m) == list and len(m) == 3 and m[0] == 'mobile'

def left(m):
    """Select the left arm of a mobile."""
    assert is_mobile(m), "must call left on a mobile"
    return m[1]

def right(m):
    """Select the right arm of a mobile."""
    assert is_mobile(m), "must call right on a mobile"
    return m[2]

Implementation of the Arm Data Abstraction (for your reference, no need to do anything here):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def arm(length, mobile_or_planet):
    """Construct a arm: a length of rod with a mobile or planet at the end."""
    assert is_mobile(mobile_or_planet) or is_planet(mobile_or_planet)
    return ['arm', length, mobile_or_planet]

def is_arm(s):
    """Return whether s is a arm."""
    return type(s) == list and len(s) == 3 and s[0] == 'arm'

def length(s):
    """Select the length of a arm."""
    assert is_arm(s), "must call length on a arm"
    return s[1]

def end(s):
    """Select the mobile or planet hanging at the end of a arm."""
    assert is_arm(s), "must call end on a arm"
    return s[2]

(Your turn!) Fill out the implementation of the Planet Data Abstraction!

1
2
3
4
5
6
7
8
9
10
11
12
13
def planet(mass):
    """Construct a planet of some mass."""
    assert mass > 0
    return ["planet",mass]

def mass(w):
    """Select the mass of a planet."""
    assert is_planet(w), 'must call mass on a planet'
    return w[1]

def is_planet(w):
    """Whether w is a planet."""
    return type(w) == list and len(w) == 2 and w[0] == 'planet'

Total Weight implementation (for your reference and understanding, no need to do anything here):

The total_weight example is provided to demonstrate use of the mobile, arm, and planet abstractions for your reference. You do not need to implement anything here. You may use the total_weight function in questions 3 and 4.

The examples function builds and returns three mobiles. These mobiles are used in the doctest examples for total_weight, a function that takes in either a mobile or a planet and returns its total weight. The total weight of a planet is just its mass. The total weight of a mobile is the sum of the masses of all the planets hanging from the mobile.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def examples():
    t = mobile(arm(1, planet(2)),
               arm(2, planet(1)))
    u = mobile(arm(5, planet(1)),
               arm(1, mobile(arm(2, planet(3)),
                              arm(3, planet(2)))))
    v = mobile(arm(4, t), arm(2, u))
    return (t, u, v)
def total_weight(m):
    """Return the total weight of m, a planet or mobile.

    >>> t, u, v = examples()
    >>> total_weight(t)
    3
    >>> total_weight(u)
    6
    >>> total_weight(v)
    9
    >>> from construct_check import check
    >>> # checking for abstraction barrier violations by banning indexing
    >>> check(HW_SOURCE_FILE, 'total_weight', ['Index'])
    True
    """
    if is_planet(m):
        return mass(m)
    else:
        assert is_mobile(m), "must get total weight of a mobile or a planet"
        return total_weight(end(left(m))) + total_weight(end(right(m)))

Use Ok to test your code:

1
python3 ok -q total_weight✂️

Q3: Balanced

Implement the balanced function, which returns whether m is a balanced mobile. A mobile is balanced if both of the following conditions are met:

  1. The torque applied by its left arm is equal to that applied by its right arm. The torque of the left arm is the length of the left rod multiplied by the total weight hanging from that rod. Likewise for the right. For example, if the left arm has a length of 5, and there is a mobile hanging at the end of the left arm of total weight 10, the torque on the left side of our mobile is 50.
  2. Each of the mobiles hanging at the end of its arms is itself balanced.

Planets themselves are balanced, as there is nothing hanging off of them.

Reminder: You may use the total_weight function defined for you in Question 2 (as well as any of the other functions defined in Question 2).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def balanced(m):
    """Return whether m is balanced.

    >>> t, u, v = examples()
    >>> balanced(t)
    True
    >>> balanced(v)
    True
    >>> w = mobile(arm(3, t), arm(2, u))
    >>> balanced(w)
    False
    >>> balanced(mobile(arm(1, v), arm(1, w)))
    False
    >>> balanced(mobile(arm(1, w), arm(1, v)))
    False
    >>> from construct_check import check
    >>> # checking for abstraction barrier violations by banning indexing
    >>> check(HW_SOURCE_FILE, 'balanced', ['Index'])
    True
    """
    if is_mobile(m):
        if total_weight(end(left(m)))*length(left(m)) != total_weight(end(right(m)))*length(right(m)):
            return False
        if not balanced(end(left(m))) or not balanced(end(right(m))):
            return False
    return True

Use Ok to test your code:

1
python3 ok -q balanced✂️

Q4: Totals

Implement totals_tree, which takes in a mobile or planet and returns a tree whose root is the total weight of the input. For a planet, totals_tree should return a leaf. For a mobile, totals_tree should return a tree whose label is that mobile‘s total weight, and whose branches are totals_trees for the ends of its arms. As a reminder, the description of the tree data abstraction can be found here.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def totals_tree(m):
    """Return a tree representing the mobile with its total weight at the root.

    >>> t, u, v = examples()
    >>> print_tree(totals_tree(t))
    3
      2
      1
    >>> print_tree(totals_tree(u))
    6
      1
      5
        3
        2
    >>> print_tree(totals_tree(v))
    9
      3
        2
        1
      6
        1
        5
          3
          2
    >>> from construct_check import check
    >>> # checking for abstraction barrier violations by banning indexing
    >>> check(HW_SOURCE_FILE, 'totals_tree', ['Index'])
    True
    """
    if is_planet(m):
        return [total_weight(m)]
    elif is_mobile(m):
        branches = []
        branches.append(totals_tree(end(left(m))))
        branches.append(totals_tree(end(right(m))))
        res = tree(total_weight(m), branches)
        return res

Use Ok to test your code:

1
python3 ok -q totals_tree✂️

More Trees

Q5: Replace Loki at Leaf

Define replace_loki_at_leaf, which takes a tree t and a value lokis_replacement. replace_loki_at_leaf returns a new tree that’s the same as t except that every leaf label equal to "loki" has been replaced with lokis_replacement.

If you want to learn about the Norse mythology referenced in this problem, you can read about it here.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def replace_loki_at_leaf(t, lokis_replacement):
    """Returns a new tree where every leaf value equal to "loki" has
    been replaced with lokis_replacement.

    >>> yggdrasil = tree('odin',
    ...                  [tree('balder',
    ...                        [tree('loki'),
    ...                         tree('freya')]),
    ...                   tree('frigg',
    ...                        [tree('loki')]),
    ...                   tree('loki',
    ...                        [tree('sif'),
    ...                         tree('loki')]),
    ...                   tree('loki')])
    >>> laerad = copy_tree(yggdrasil) # copy yggdrasil for testing purposes
    >>> print_tree(replace_loki_at_leaf(yggdrasil, 'freya'))
    odin
      balder
        freya
        freya
      frigg
        freya
      loki
        sif
        freya
      freya
    >>> laerad == yggdrasil # Make sure original tree is unmodified
    True
    """
    if is_leaf(t):
        if label(t)=="loki":
            return tree(lokis_replacement)
    return tree(label(t),[replace_loki_at_leaf(x, lokis_replacement) for x in branches(t)])

Use Ok to test your code:

1
python3 ok -q replace_loki_at_leaf✂️

Q6: Has Path

Write a function has_path that takes in a tree t and a string word. It returns True if there is a path that starts from the root where the entries along the path spell out the word, and False otherwise. (This data structure is called a trie, and it has a lot of cool applications, such as autocomplete). You may assume that every node’s label is exactly one character.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def has_path(t, word):
    """Return whether there is a path in a tree where the entries along the path
    spell out a particular word.

    >>> greetings = tree('h', [tree('i'),
    ...                        tree('e', [tree('l', [tree('l', [tree('o')])]),
    ...                                   tree('y')])])
    >>> print_tree(greetings)
    h
      i
      e
        l
          l
            o
        y
    >>> has_path(greetings, 'h')
    True
    >>> has_path(greetings, 'i')
    False
    >>> has_path(greetings, 'hi')
    True
    >>> has_path(greetings, 'hello')
    True
    >>> has_path(greetings, 'hey')
    True
    >>> has_path(greetings, 'bye')
    False
    >>> has_path(greetings, 'hint')
    False
    """
    assert len(word) > 0, 'no path for empty word.'
    if len(word) == 1:
        if(label(t)==word[0]):
            return True
        return False
    else:
        if(label(t)==word[0]):
            for i in branches(t):
                if has_path(i, word[1:]):
                    return True
            return False
        else:
            return False

Use Ok to test your code:

1
python3 ok -q has_path✂️

Optional Questions

Data Abstraction

Feel free to reference Section 2.2 for more information on data abstraction.

Acknowledgements. This interval arithmetic example is based on a classic problem from Structure and Interpretation of Computer Programs, Section 2.1.4.

Introduction. Alyssa P. Hacker is designing a system to help people solve engineering problems. One feature she wants to provide in her system is the ability to manipulate inexact quantities (such as measurements from physical devices) with known precision, so that when computations are done with such approximate quantities the results will be numbers of known precision. For example, if a measured quantity x lies between two numbers a and b, Alyssa would like her system to use this range in computations involving x.

Alyssa’s idea is to implement interval arithmetic as a set of arithmetic operations for combining “intervals” (objects that represent the range of possible values of an inexact quantity). The result of adding, subracting, multiplying, or dividing two intervals is also an interval, one that represents the range of the result.

Alyssa suggests the existence of an abstraction called an “interval” that has two endpoints: a lower bound and an upper bound. She also presumes that, given the endpoints of an interval, she can create the interval using data abstraction. Using this constructor and the appropriate selectors, she defines the following operations:

1
2
3
4
5
6
7
8
9
10
def str_interval(x):
    """Return a string representation of interval x."""
    return '{0} to {1}'.format(lower_bound(x), upper_bound(x))

def add_interval(x, y):
    """Return an interval that contains the sum of any value in interval x and
    any value in interval y."""
    lower = lower_bound(x) + lower_bound(y)
    upper = upper_bound(x) + upper_bound(y)
    return interval(lower, upper)

Q7: Interval Abstraction

Alyssa’s program is incomplete because she has not specified the implementation of the interval abstraction. She has implemented the constructor for you; fill in the implementation of the selectors.

1
2
3
4
5
6
7
8
9
10
11
12
def interval(a, b):
    """Construct an interval from a to b."""
    assert a <= b, 'Lower bound cannot be greater than upper bound'
    return [a, b]

def lower_bound(x):
    """Return the lower bound of interval x."""
    return x[0]

def upper_bound(x):
    """Return the upper bound of interval x."""
    return x[1]

Use Ok to unlock and test your code:

1
2
python3 ok -q interval -u
python3 ok -q interval✂️

Q8: Interval Arithmetic

After implementing the abstraction, Alyssa decided to implement a few interval arithmetic functions.

This is her current implementation for interval multiplication. Unfortunately there are some data abstraction violations, so your task is to fix this code before someone sets it on fire.

1
2
3
4
5
6
7
8
def mul_interval(x, y):
    """Return the interval that contains the product of any value in x and any
    value in y."""
    p1 = x[0] * y[0]
    p2 = x[0] * y[1]
    p3 = x[1] * y[0]
    p4 = x[1] * y[1]
    return [min(p1, p2, p3, p4), max(p1, p2, p3, p4)]

Use Ok to unlock and test your code:

1
2
python3 ok -q mul_interval -u
python3 ok -q mul_interval✂️

Interval Subtraction

Using a similar approach as mul_interval and add_interval, define a subtraction function for intervals. If you find yourself repeating code, see if you can reuse functions that have already been implemented.

1
2
3
4
5
6
def sub_interval(x, y):
    """Return the interval that contains the difference between any value in x
    and any value in y."""
    lower = lower_bound(x) - upper_bound(y)
    upper = upper_bound(x) - lower_bound(y)
    return interval(lower, upper)

Use Ok to unlock and test your code:

1
2
python3 ok -q sub_interval -u
python3 ok -q sub_interval✂️

Interval Division

Alyssa implements division below by multiplying by the reciprocal of y. A systems programmer looks over Alyssa’s shoulder and comments that it is not clear what it means to divide by an interval that spans zero. Add an assert statement to Alyssa’s code to ensure that no such interval is used as a divisor:

1
2
3
4
5
6
7
def div_interval(x, y):
    """Return the interval that contains the quotient of any value in x divided by
    any value in y. Division is implemented as the multiplication of x by the
    reciprocal of y."""
    assert lower_bound(y)>0 or upper_bound(y)<0
    reciprocal_y = interval(1 / upper_bound(y), 1 / lower_bound(y))
    return mul_interval(x, reciprocal_y)

Use Ok to unlock and test your code:

1
2
python3 ok -q div_interval -u
python3 ok -q div_interval✂️

Q9: Par Diff

After considerable work, Alyssa P. Hacker delivers her finished system. Several years later, after she has forgotten all about it, she gets a frenzied call from an irate user, Lem E. Tweakit. It seems that Lem has noticed that the formula for parallel resistors can be written in two algebraically equivalent ways:

1
par1(r1, r2) = (r1 * r2) / (r1 + r2)

or

1
par2(r1, r2) = 1 / (1/r1 + 1/r2)

He has written the following two programs, each of which computes the parallel_resistors formula differently:

1
2
3
4
5
6
7
8
def par1(r1, r2):
    return div_interval(mul_interval(r1, r2), add_interval(r1, r2))

def par2(r1, r2):
    one = interval(1, 1)
    rep_r1 = div_interval(one, r1)
    rep_r2 = div_interval(one, r2)
    return div_interval(one, add_interval(rep_r1, rep_r2))

Lem points out that Alyssa’s program gives different answers for the two ways of computing. Find two intervals r1 and r2 that demonstrate the difference in behavior between par1 and par2 when passed into each of the two functions.

Demonstrate that Lem is right. Investigate the behavior of the system on a variety of arithmetic expressions. Make some intervals r1 and r2, and show that par1 and par2 can give different results.

1
2
3
4
5
6
7
8
9
10
11
12
def check_par():
    """Return two intervals that give different results for parallel resistors.

    >>> r1, r2 = check_par()
    >>> x = par1(r1, r2)
    >>> y = par2(r1, r2)
    >>> lower_bound(x) != lower_bound(y) or upper_bound(x) != upper_bound(y)
    True
    """
    r1 = interval(7, 123)  # Replace this line!
    r2 = interval(3, 44)  # Replace this line!
    return r1, r2
CS61A Homework 4
2023/09/05/CS61A Homework 4/
Author
easterling
Published
2023-09-05 21:55
License
 Comments
Comment plugin failed to load
Loading comment plugin
  1. 1. Homework 4: Sequences, Trees hw04.zip
  2. 2. Required questions
    1. 2.1. Arms-length recursion
    2. 2.2. Mobiles
      1. 2.2.1. Q2: Weights
      2. 2.2.2. Q3: Balanced
      3. 2.2.3. Q4: Totals
    3. 2.3. More Trees
      1. 2.3.1. Q5: Replace Loki at Leaf
      2. 2.3.2. Q6: Has Path
  3. 3. Optional Questions
    1. 3.1. Data Abstraction
      1. 3.1.1. Q7: Interval Abstraction
      2. 3.1.2. Q8: Interval Arithmetic
      3. 3.1.3. Q9: Par Diff